Numerical analysis applies to many processes that occur in the real-world that can be modeled by mathematical equations. Unfortunately, many of these equations, while seemingly simple, cannot be solved directly by known analytical methods. The techniques taught in algebra, trigonometry, and calculus courses, while extremely powerful, apply to only a small fraction of the complex real-world models that researchers encounter.

Numerical analysis takes care of the rest. For many models where it is difficult to find the answer, but easy to verify it, numerical analysis can be used to produce an approximation as precise as we want. Numerical techniques generally involve clever techniques to successively improve guesses at the answer or convert the model into a system of equations which can be solved directly. Both of these methods are tedious to perform by hand, but well-suited to a fast computer.

The classic first example often used in numerical analysis courses is Newton's method for estimating the roots of an equation (where the graph of the equation crosses the x axis). The aim is to answer the question: "For what value(s) of x does f(x) = 0?".

While finding the roots of some equations is not easy to do directly, it is generally easy to compute f(x) for any value of x and see how close it is to 0.

Now for the clever part: In most cases, a line tangent to f(x) will cross the x-axis at a point closer to a root than x. This can be visualized by drawing a graph of an arbitrary function, and a series of tangent lines.

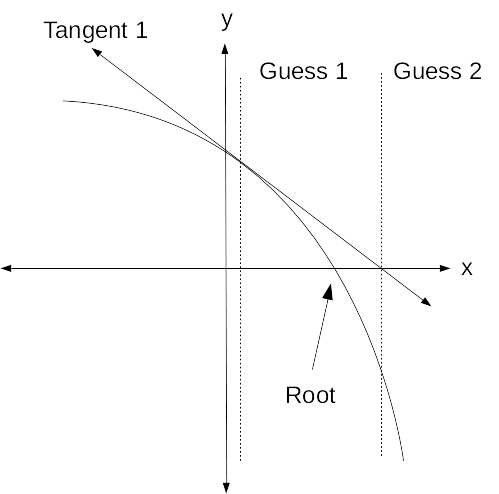The equation for the tangent line is easily computed using x, f(x), and f'(x), the slope of the curve at f(x). The root of the tangent line (where the tangent line crosses the x axis) is then easily calculated using the equation for the line. This becomes the next "guess" for the root of the equation. With rare exceptions, this next guess for x will be closer to the root than the previous x. We continue this process until f(x) is sufficiently close to 0 or until the difference between subsequent guesses at x is sufficiently small.

Computational models simulate real-world processes, following the relevant laws of math and physics.

Models might simulate the motion of individual molecules in a fluid or solid, or larger cells of fluid such as oil in an engine, water in the ocean, or air in the atmosphere. The weather forecasts we rely on (and complain about) are determined mainly through the use of large-scale fluid models utilizing measurements of temperature, pressure, humidity, and wind throughout the planet.

Models are also used to simulate traffic flow on roads and expressways that have not yet been built, usage patterns in buildings still in design phase, and population growth and collapse in remote ecosystems, to mention just a few more cases. Scientists, engineers and architects use models to find out things in advance that could otherwise get them in trouble, like "Will closing a lane during rush hour cause a traffic jam?" or "What will happen if we only put a bathroom on every other floor?".

The term "mining" traditionally refers to digging through vast amounts of earth to find small amounts of valuable minerals. The minerals are generally a very small fraction of the earth that's removed, and it requires a lot of work to find and separate them.

There are also vast amounts of data stored on computers that contain small amounts of information of interest to a particular researcher. Data mining is the process of sifting through these data for "interesting" information.

There are many possible approaches to data mining. The ultimate goal is to have a computer search through huge archives or databases of information without human intervention and automatically identify items or patterns of interest. This is not always feasible, so a more practical goal is often to have the computer do as much as possible and simply minimize the human labor involved.

Depending on the type of information being searched, teaching a computer to identify truly interesting patterns can be fairly difficult and may require the use of artificial intelligence techniques. For example, a now-famous data mining experiment used to search hospital records for patterns initially reported that all of the maternity ward patients were women.

This underscores the fact that while computers are powerful tools that can do many things far faster and more accurately than humans, there are still many tasks that require human knowledge and reasoning.

Numerical analysis uses techniques to progressively improve guesses at the solution to a problem. Unfortunately, sometimes we can't come up with a clever method of improving on our current guess and we simply have to test every possible answer until we find one that works.

A parameter sweep tests a range of possible answers to a question, until at least one correct answer is found, or until all possible answers have been checked in order to determine a near-optimal set of parameters. It is a brute-force approach to answering questions where directly computing the answer is not feasible.

It may involve repeating a set of calculations with numerous combinations of multiple parameters in order to determine the optimal set of parameters.

An example involving a single parameter is the brute-force password hack. Passwords are stored in an encrypted form that cannot be directly converted back to the raw password. Since it is the raw password that must be entered in order to log into a computer, this effectively prevents unauthorized access even if the encrypted passwords are known. This is important since many passwords must be transmitted over networks in order to log into remote systems such as email servers. Hence, it is often difficult or impossible to prevent encrypted passwords from becoming known.

While it is practically impossible to decrypt a password, it is relatively straightforward to encrypt a guess and see if it matches the known encrypted form.

The main defense against this type of brute-force attack is forcing the attacker to try more guesses, i.e. maximizing the parameter space that must be swept. An 8-character password randomly consisting of both upper and lower case English letters, digits, and punctuation has (26 + 26 + 10 + 32)⁸ = 6.09 x 10¹⁵ possible patterns (based on a US-English keyboard).

If a computer can encrypt and compare 100,000 guesses per second, it will take 1,932 years to sweep the entire parameter space. On average, it will take half that time to find one particular password with these qualities.

On the other hand, if the attacker knows that your password is a 10-letter English word with a mix of upper and lower case, then based on the size of the Oxford English dictionary (about 170,000 words), there are only about (170,000 * 2¹⁰) = 174,080,000 possible passwords. At 100,000 guesses per second, it would take the hacker's tools at most 1741 seconds = 29 minutes to find your raw password.

For this reason, a password should never be any kind of derivative of a real word.

The worst kind of password, of course, is anything containing personal information. Many computer users think they're outsmarting hackers by putting a digit or two after their name to form a "secure" password. Hackers have a standard list of items commonly used by people just begging to get hacked, such as their name, birthday, pet's name, favorite color, etc. Most of this information is readily available online thanks to sites like Facebook. Checking every item in this list followed by every possible number from 1 to 999 (e.g. from azure0 to zebra999) will take only a fraction of a second on a modern computer.

In some cases, there are just gobs and gobs of raw data to be sifted and checked for known or expected patterns. This is different from data mining in the sense that the human programmers know what to look for.

Examples of this type of computational research are well illustrated by the @home projects, such as Einstein@Home, which searches data from laser interferometer gravitational-wave observatory (LIGO) detectors for evidence of gravity waves. The LIGO detectors unfortunately don't beep when they spot a gravity wave. Instead, they generate enormous amounts of data, most of which will not show any evidence of gravity waves, but nevertheless must be examined thoroughly. The Einstein@Home project uses massive numbers of personal computers around the world, each sweeping a small segment of the LIGO raw data.

Monte Carlo simulations, named after the gambling city in the French Riviera, utilize random numbers and simulation to piece together answers to scientific questions.

The method actually looks similar to a parameter sweep or data sift in that the same calculations are done on a large number of different inputs. However, the Monte Carlo method uses random inputs rather than a predetermined set of inputs. The random numbers generated are generally designed to be representative of the entire possible range, while being a fraction of the size.

For example, the average of a small, but truly random sample of a population is generally very close to the true average of the entire population. This mathematical fact makes many experiments possible in the humanities and social sciences, where sampling every member of a society is practically impossible.

A classic example of the Monte Carlo method is the estimation of the value of pi using a dart board.

Suppose we have a square dart board with a circle inscribed:

The area of the circle is PI * (1/2)² = PI/4. The area of the square is 1. The ratio of the area of the circle over the area of the square is therefore PI/4.

If a bad enough darts player throws a large number of darts at the board, darts will end up randomly and uniformly distributed across the square board (and probably the surrounding wall). If and only if the darts are randomly and uniformly distributed, the ratio of the number of darts within the inscribed circle over the number of darts within the entire square board will then be close to pi/4.

Statistically, the more darts are thrown, the closer the ratio will get to pi.

Naturally, this process would take too long with a real dart board, so we might instead choose to simulate it on a computer. Most programming languages offer the ability to generate pseudo-random numbers within some fixed range with a uniform distribution. By randomly generating a sequence of x and y values with a uniform distribution, we can rapidly simulate throwing darts at a board and quickly develop an estimate for pi.

The previous sections outline some of the commonly used methods in computational science.

Researchers can explore and understand these methods and also discover or invent new methods of their own for using computers in their research. The computational capacity of today's computers is both vast and vastly underutilized. The possibilities for computational research are almost limitless and bounded only by the skills and imagination of the researcher.

It is our hope that more researchers will simply begin to consider how computational methods might improve their research and then develop the skills and knowledge to tap into the vast and freely available hardware and software resources that are waiting to be utilized.